哈夫曼树的介绍及C语言代码实现
1. 简介
哈夫曼树(Huffman Tree),又名:最优二叉树,赫夫曼树
其标准含义是:给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
2. 相关名词
由于本篇存在一定的难度,因此在开始相关的学习之前,请让我们来巩固以下本文所涉及的名词知识点。
a) 路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径。
b) 路径长度:在一条路径中,每经过一个结点,路径长度都要加 1 。例如在一棵树中,规定根结点所在层数为1层,那么从根结点到第 i 层结点的路径长度为 i - 1 。
c) 结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权。
d) 结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。
e) 树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL”。
3.构建哈夫曼树
在构建哈夫曼树时,只需要遵循一个原则,那就是权重越大的结点距离树根越近。
因此,在构建过程中,有如下的规律:
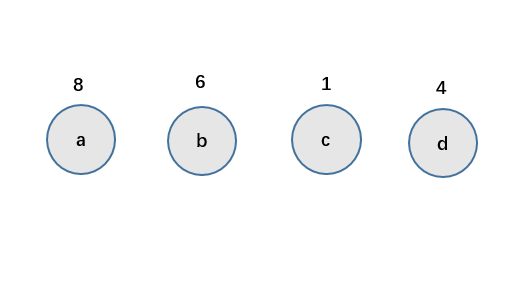
首先,选出我们数据中最小的两个数据,构建成二叉树的左孩子和右孩子,而根的数据为两者之和
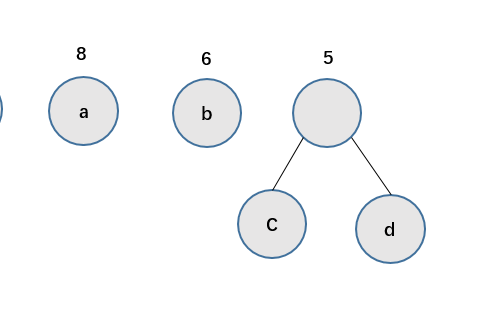
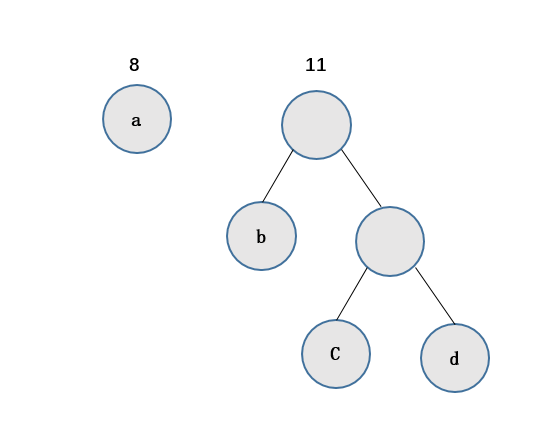
其次,将刚才合成的数据作为右孩子,左孩子从未处理的数据中选出最小的一个,作为左孩子,他们的根同样为左右孩子的权值和
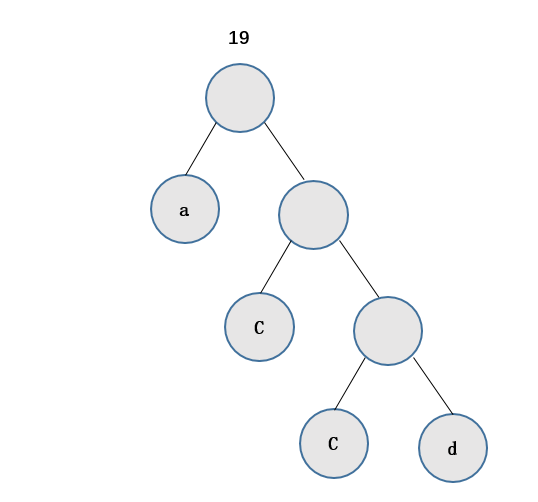
不断重复上述的步骤,直到将所有的数据全部处理完并构建出二叉树,这棵二叉树就是我们的哈夫曼树。
如图这颗哈夫曼树的WPL值为:WPL= 8*1+ 6*2 + 1*3 + 4*3 = 273
4. 哈夫曼树的结点结构
与一般的二叉树并没有什么实质的不同,甚至可以说结构都完全一致,由于性值,因此其需要利用parent进行访问双亲结点
其代码表示为:
//哈夫曼树结点结构
typedef struct {
int weight; //结点权重
int parent, left, right; //父结点、左孩子、右孩子在数组中的位置下标
} HTNode, *HuffmanTree;其中weight为结点权重,
5.构建哈夫曼树
由上文的分析可知,构建哈夫曼树时,我们需要根据各个结点的权重值,筛选出其中值最小的两个结点,构建二叉树。
其代码为:
//HT为地址传递的存储哈夫曼树的数组,w为存储结点权重值的数组,n为结点个数
void CreateHuffmanTree(HuffmanTree *HT, int *w, int n) {
if(n <= 1)
return; // 如果只有一个编码就相当于0
int m = 2*n-1; // 哈夫曼树总节点数,n就是叶子结点
*HT = (HuffmanTree)malloc((m+1) * sizeof(HTNode)); // 0号位置不用
HuffmanTree p = *HT;
// 初始化哈夫曼树中的所有结点
for(int i = 1; i <= n; i++) {
(p+i)->weight = *(w+i-1);
(p+i)->parent = 0;
(p+i)->left = 0;
(p+i)->right = 0;
}
//从树组的下标 n+1 开始初始化哈夫曼树中除叶子结点外的结点
for(int i = n+1; i <= m; i++) {
(p+i)->weight = 0;
(p+i)->parent = 0;
(p+i)->left = 0;
(p+i)->right = 0;
}
//构建哈夫曼树
for(int i = n+1; i <= m; i++) {
int s1, s2;
Select(*HT, i-1, &s1, &s2); //查找内容,需要用到查找算法
(*HT)[s1].parent = (*HT)[s2].parent = i;
(*HT)[i].left = s1;
(*HT)[i].right = s2;
(*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;
}
}本文固定URL:https://www.dotcpp.com/course/143