图的遍历BFS广度优先搜索
1. 简介
BFS(Breadth First Search,广度优先搜索,又名宽度优先搜索),与深度优先算法在一个结点“死磕到底“的思维不同,广度优先算法关注的重点在于每一层的结点进行的下一层的访问。
2. BFS算法介绍
BFS算法和核心思路就是:从某个点一直把其邻接点走完,然后任选一个邻接点把与之邻接的未被遍历的点走完,如此反复走完所有结点。类似于树的层序遍历。
BFS的核心就是要把当前在哪作为一个状态存储,并将这个状态交给队列进行入队操作,故而,
算法步骤(用队列实现)
a) 访问指定起始点。
b) 访问当前顶点的邻接顶点有未被访问的顶点,并将之放入队列中。
c) 删除队列的队首节点。访问当前队列的队首,前面的步骤。直到队列为空。
d) 若若途中还有顶点未被访问,则再选一个点作为起始顶点。重复前面的步骤。(针对非连通图)。
3. 案例图示
还是这一份例图,我们直接以案例进行讲解,就本图而言,其访问顺序可以是(不唯一):1-2-3-4-5
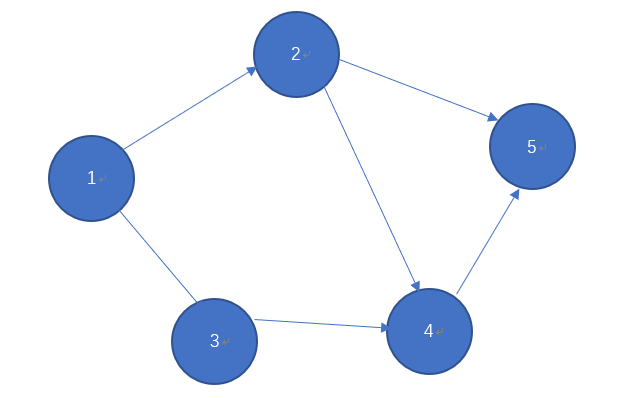
首先从1开始,1结点处可以访问2,3两个结点,我们访问并以此把两个结点的访问顺序放入队列,然后按照入队顺序(如2,3),之后我们出队状态2,依次访问2结点的下两个结点(4,5结点),并入队4,5结点,再之后我们出队3结点,并依次访问后续,此时发现所有的结点已经被访问完毕了,可以结束搜索,最后我们得到次序:1-2-3-4-5
4. 相关代码
BFS的模板代码如下:
/**
* 返回合适的检索数据
*/
int BFS(Node root, Node target)
{
Queue<Node> queue; //创建队列
int step = 0; // 当前队列的步骤点
// initialize
add root to queue;
// BFS
while (queue is not empty)
{
step = step + 1;
//步数逐渐增加
int size = queue.size();
for (int i = 0; i < size; ++i)
{
Node cur = the first node in queue;
if cur is target
return step - 1;
for (Node next : the neighbors of cur)
{//这里常用一个二维方向数组实现
add next to queue;
}
remove the first node from queue;
}
}
return -1; //出错返回值
}同样提供一份BFS的图论算法节选,代码最核心还是取记忆BFS的模板并根据实际情况的灵活使用,故以下代码仅提供参考
void BFSL(int pos,pGraph G,int visited[30])//从pos点开始进行广度优先遍历无向图
{
int queue[G->Vnum];//队列辅助BFS遍历
int head=0,tail=0;//队头、队尾指针
Arcnode* p;
queue[tail]=pos;
visited[pos]=1;//标记遍历过
tail++;
while(head!=tail)
{
pos=queue[head];//出队操作
head++;
printf("%d ",pos);
p=G->vertice[pos].firstarc;
while(p!=NULL)
{
if(visited[p->adjvex]==0)//判断是否遍历过
{
queue[tail]=p->adjvex;//入队操作
visited[p->adjvex]=1;//标记遍历过
tail++;
}
p=p->next;
}
}
}5. 应用
BFS算法的实际应用场景,最典型的有地图搜索,迷宫寻路等,需要有“状态”以及状态改变场景的搜索算法,同时BFS由于不需要像DFS算法那样回溯,故比DFS效率可能会更高一些。基于BFS算法的该进算法,比如说R星寻路,DBFS(双向广搜)算法等这类改进算法场景被应用在实际游戏设计,GPS导航设计等场景中。
本文固定URL:https://www.dotcpp.com/course/149