Dotcpp  /  编程题库  /   [CSP-J 2024] 4 接龙
题目 1748:

[CSP-J 2024] 4 接龙

 时间限制: 1s 内存限制: 128MB
题目描述

在玩惯了成语接龙之后，小 J 和他的朋友们发明了一个新的接龙规则。

总共有 n 个人参与这个接龙游戏，第 i 个人会获得一个整数序列 Si 作为他的词库。

一次游戏分为若干轮，每一轮规则如下：

n 个人中的某个人 p 带着他的词库 Sp 进行接龙。若这不是游戏的第一轮，那么这一轮进行接龙的人不能与上一轮相同，但可以与上上轮或更往前的轮相同。

接龙的人选择一个长度在 [2,k] 的 Sp 的连续子序列 A 作为这一轮的接龙序列，其中 k 是给定的常数。若这是游戏的第一轮，那么 A 需要以元素 1 开头，否则 A 需要以上一轮的接龙序列的最后一个元素开头。

序列 A 是序列 S 的连续子序列当且仅当可以通过删除 S 的开头和结尾的若干元素（可以不删除）得到 A。

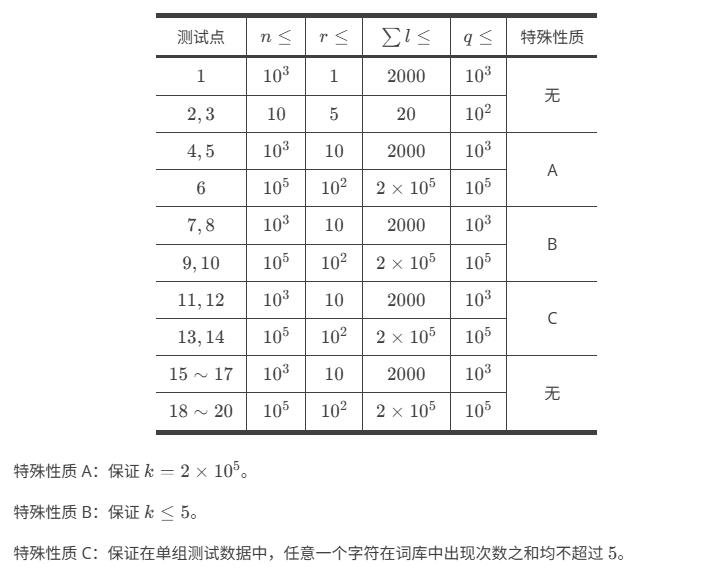
为了强调合作，小 J 给了 n 个参与游戏的人 q 个任务，第 j 个任务需要这 n 个人进行一次游戏，在这次游戏里进行恰好 rj 轮接龙，且最后一轮的接龙序列的最后一个元素恰好为 cj。为了保证任务的可行性，小 J 请来你判断这 q 个任务是否可以完成的，即是否存在一个可能的游戏过程满足任务条件。


输入

输入的第一行包含一个正整数 T，表示数据组数。

接下来包含 T 组数据，每组数据的格式如下：

第一行包含三个整数 n,k,q，分别表示参与游戏的人数、接龙序列长度上限以及任务个数。

接下来 n 行：

第 i 行包含 (li+1) 个整数 li,Si,1,Si,2,…,Si,li，其中第一个整数 li 表示序列 Si 的长度，接下来 li 个整数描述序列 Si。

接下来 q 行：

第 j 行包含两个整数 rj,cj，描述一个任务。


输出

对于每个任务：输出一行包含一个整数，若任务可以完成输出 1，否则输出 0。

样例输入

1
3 3 7
5 1 2 3 4 1
3 1 2 5
3 5 1 6
1 2
1 4
2 4
3 4
6 6
1 1
7 7

样例输出

1
0
1
0
1
0
0
提示

【样例 1 解释】

在下文中，我们使用 {Ai}={A1,A2,…,Ar} 表示一轮游戏中所有的接龙序列，{pi}={p1,p2,…,pr} 表示对应的接龙的人的编号。由于所有字符均为一位数字，为了方便我们直接使用数字字符串表示序列。

对于第一组询问，p1=1、A1=12 是一个满足条件的游戏过程。

对于第二组询问，可以证明任务不可完成。注意 p1=1、A1=1234 不是合法的游戏过程，因为此时 ∣A1∣=4>k。

对于第三组询问，{pi}={2,1}、{Ai}={12,234} 是一个满足条件的游戏过程。

对于第四组询问，可以证明任务不可完成。注意 {pi}={2,1,1}、{Ai}={12,23,34} 不是一个合法的游戏过程，因为尽管所有的接龙序列长度均不超过 k，但第二轮和第三轮由同一个人接龙，不符合要求。

对于第五组询问，{pi}={1,2,3,1,2,3}、{Ai}={12,25,51,12,25,516} 是一个满足条件的游戏过程。

对于第六组询问，可以证明任务不可完成。注意每个接龙序列的长度必须大于等于 2，因此 A1=1 不是一个合法的游戏过程。

对于第七组询问，所有人的词库均不存在字符 7，因此任务显然不可完成。


360截图20250930162758395.jpg

360截图20250930162758395.jpg


通过率

统　计

　提交 4
　正确 1
　格式错误 0
　答案错误 0
　时间超限 3
　内存超限 0
　输出超限 0
　运行错误 0
　编译错误 0