Dotcpp  /  编程题库  /   [CSP-J 2023] 3 一元二次方程
题目 1751:

[CSP-J 2023] 3 一元二次方程

 时间限制: 1s 内存限制: 128MB
题目描述

360截图20250930162758395.jpg

现在给定一个一元二次方程的系数 a,b,c，其中 a,b,c 均为整数且 a=0。你需要判断一元二次方程 ax2+bx+c=0 是否有实数解，并按要求的格式输出。

在本题中输出有理数 v 时须遵循以下规则：

由有理数的定义，存在唯一的两个整数 p 和 q，满足 q>0，gcd(p,q)=1 且 v=qp。

若 q=1，则输出 {p}，否则输出 {p}/{q}，其中 {n} 代表整数 n 的值；

例如：

当 v=−0.5 时，p 和 q 的值分别为 −1 和 2，则应输出 -1/2；

当 v=0 时，p 和 q 的值分别为 0 和 1，则应输出 0。

360截图20250930162758395.jpg

360截图20250930231848353.jpg

输入

输入的第一行包含两个正整数 T,M，分别表示方程数和系数的绝对值上限。

接下来 T 行，每行包含三个整数 a,b,c。


输出

输出 T 行，每行包含一个字符串，表示对应询问的答案，格式如题面所述。

样例输入

9 1000
1 -1 0
-1 -1 -1
1 -2 1
1 5 4
4 4 1
1 0 -432
1 -3 1
2 -4 1
1 7 1

样例输出

1
NO
1
-1
-1/2
12*sqrt(3)
3/2+sqrt(5)/2
1+sqrt(2)/2
-7/2+3*sqrt(5)/2
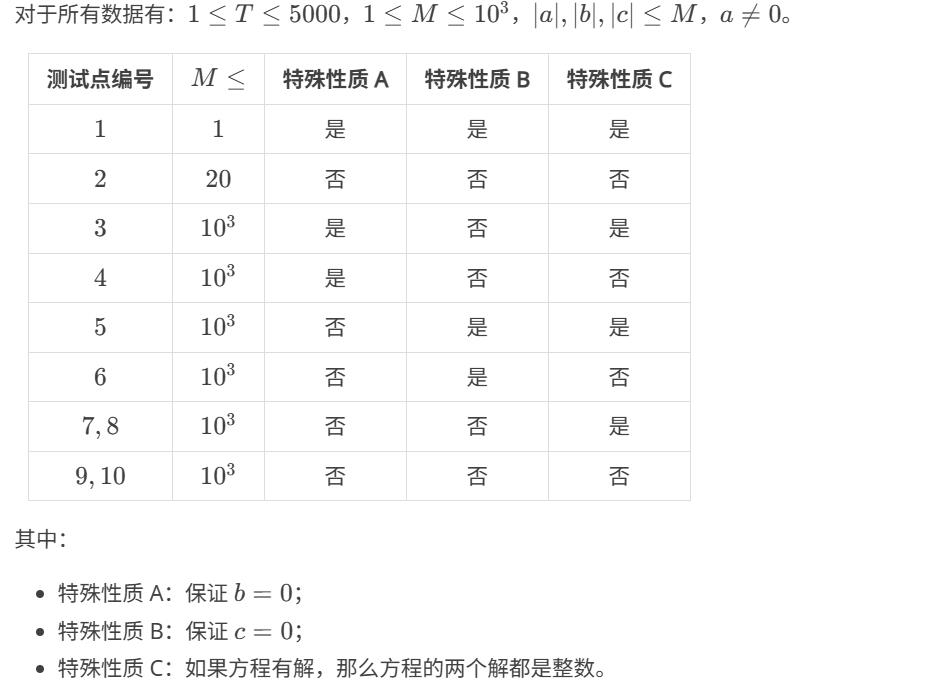
提示

360截图20250930233240519.jpg

通过率

统　计

　提交 2
　正确 1
　格式错误 0
　答案错误 1
　时间超限 0
　内存超限 0
　输出超限 0
　运行错误 0
　编译错误 0