树的遍历之中序遍历二叉树
1. 简介
依旧是下面的这三句话:
先序遍历:根左右
中序遍历:左根右
后序遍历:左右根
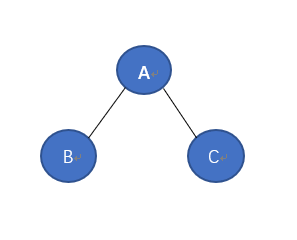
在上文我们接触到了先序遍历,本文我们开始学习中序遍历,中序遍历采用左根右的遍历方式,如图,就一个最简单的二叉树遍历而言,中序遍历的遍历访问过程是先B再A再C。
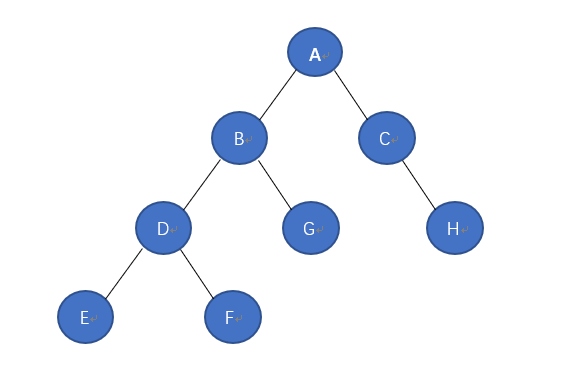
实际上的二叉树并没有这么简单,其应该是由多个结点构成的,如图所示,进行第一次访问的时候,我们在ABC中进行遍历,由左根右的顺序,我们遍历访问到B,这时候先别急,B同时又作为BDG的根结点,因此需要继续向下进行遍历,此时我们遍历到DEF,这时E属于这一组之中的左结点,因此我们根据根左右的先后顺序得到了最先的遍历效果,EDF,这EDF同时作为BDG中的左节点(把EDF看作一个整体)进行回溯,此时的访问的结点顺序为EDFBG同理, EDFBG作为ABC的左结点根据左根右的顺序EDFBGAC,左半部分访问完毕接着访问右半部分,我们将^CH(^表示空)看作一组左中右,而C就是由EDFBGAC组合而成,因此最终的遍历顺序为:EDFBGACH
2. 代码实现
续上文的代码,巧妙利用递归,与前文的代码只有一个顺序的区别:
//树的中序遍历 In-order traversal
void inorder(Node* node){
if (node != NULL)
{
inorder(node->left);
printf("%d ",node->data);
inorder(node->right);
}
}3. 中缀表达式(常规算式)
中缀表达式是一个通用的算术或逻辑公式表示方法。中缀表达式就是我们最常用的表达式形式,也是人最容易理解的表达式形式。
如图,为常规表达式:(a+b)*c
其二叉树的表现形式为: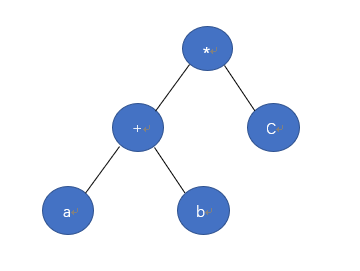
由前文可知波兰式的表达方式就是 *+cab ,我们常规的表达式的计算是中序的,其表达式就是(a+b)*c,我们可以理解为将表达式利用二叉树化,然后通过中序遍历的方式进行提取,如果需要发生组合时,需要我们借助括号的形式表示优先级,这样也有一个弊端,就是当多个嵌套的时候需要的括号较多。
4. 相关问题
l 二叉树的遍历习题:1734题
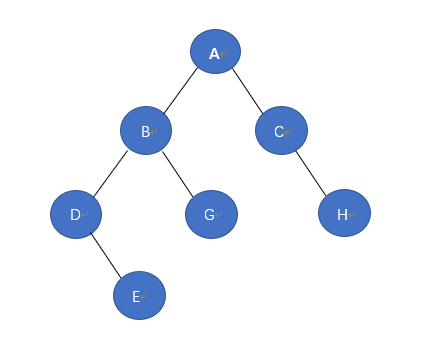
请回答这一颗树的中序遍历是多少?
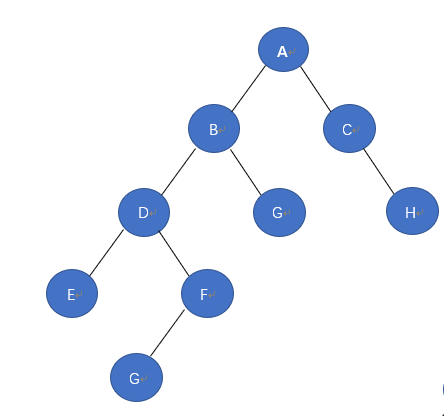
l 请回答这一颗二叉树的中序遍历是多少?
l 请回答((a+b)+(c+d))*e作为中缀表达式的二叉树如何,做图表示。
| 1734 | 二叉树遍历 |
本文固定URL:https://www.dotcpp.com/course/138