树上启发式合并

启发式算法是什么呢？启发式算法是基于人类的经验和直观感觉，对一些算法的优化。

最常见的就是并查集的按秩合并了，有带按秩合并的并查集中，合并的代码是这样的：

void merge(int x, int y) {
  int xx = find(x), yy = find(y);
  if (size[xx] < size[yy]) swap(xx, yy);
  fa[yy] = xx;
  size[xx] += size[yy];
}

在这里，对于两个大小不一样的集合，我们将小的集合合并到大的集合中，而不是将大的集合合并到小的集合中。

让高度小的树成为高度较大的树的子树，这个优化可以称为启发式合并算法。

树上启发式合并（dsu on tree）对于某些树上离线问题可以速度大于等于大部分算法且更易于理解和实现的算法。

他是用来解决一类树上询问问题，一般这种问题有两个特征：

（1）只有对子树的询问

（2）没有修改

例题：给出一棵n个节点以1为根的树，节点u的颜色为cu ，现在对于每个结点u询问u子树里一共出现了多少种不同的颜色。

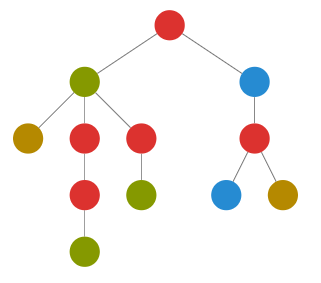
对于这种问题解决方式大多是运用大量的数据结构（树套树等），如果可以离线，询问的量巨大，是不是有更简单的方法？

树套树可以解决，如果可以离线的话，树上莫队复杂度带根号，现在我们要用一个带log的算法。对于直接暴力复杂度为，即对每一个子节点进行一次遍历，对于每个节点的答案是由其子树和其本身得到的，现在考虑利用这个性质处理问题。

我们预处理出每个节点子树的大小和其重儿子，重儿子同树链剖分一样，都是拥有节点最多子树的儿子，这个过程O(n)求。

用cnt[i]表示颜色i出现的次数，ans[u]表示节点u的答案。

遍历一个节点u，我们按以下步骤遍历：

（1）先遍历u的轻（非重）儿子，并计算答案，但 不保留遍历后它对 cnt 数组的影响；

（2）遍历它的重儿子，保留它对 cnt 数组的影响；

（3）再次遍历u的轻儿子的子树结点，加入这些结点的贡献，以得到u的答案。

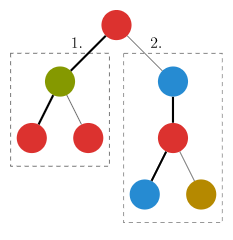
上图是一个例子。

这样，对于一个节点，我们遍历了一次重子树，两次非重子树，显然是最划算的。

通过执行这个过程，我们获得了这个节点所有子树的答案。

为什么不合并第一步和第三步呢，因为cnt数组不能重复使用，不然空间复杂度太高，需要O(n)内完成

若一个节点u被遍历了x次，则其重儿子被遍历x次，轻儿子（如果有的话）被遍历2x次

这样的复杂度是O(nlog n)

注意除了重儿子，每次遍历完 cnt 要清零。

int sz[N],son[N];

void dfs1(int x){
    /* 求解重儿子 */
    sz[x] = 1;
    for(int i = head[x]; i; i = e[i].next){
        int y = e[i].to;
        dfs1(y); sz[x] += sz[y];
        if(sz[y] > sz[son[x]]) son[x] = y;
    }
}

void Delete(int x){
    /* 删除的内容 */
    for(int i = head[x]; i; i = e[i].next) Delete(e[i].to);
}

void modify(int x,int fa){
    /* 更新的内容 */
    for(int i = head[x]; i; i = e[i].next) modify(e[i].to,fa);
}

void ins(int x){
    /* 插入的内容 */
    for(int i = head[x]; i; i = e[i].next) ins(e[i].to);
}

void dfs2(int x){
    /* 求解轻儿子并清空 */
    for(int i = head[x]; i; i = e[i].next)
        if(e[i].to != son[x]) dfs2(e[i].to), Delete(e[i].to);

    /* 求解重儿子并保留 */
    if(son[x]) dfs2(son[x]);
    /* 用重儿子更新答案 */

    /* 枚举轻儿子更新答案，并加入轻儿子 */
    for(int i = head[x]; i; i = e[i].next) 
        if(e[i].to != son[x]) modify(e[i].to,x), ins(e[i].to);

    /* 用所有儿子更新答案 */
}

证明：

性质：一个节点到根的路径上轻边个数不会超过logn条

我们考虑一个点会被访问几次？

一个点被访问只有两种情况：

①在暴力统计轻边的时候访问到，次数<logn

②通过重边/在遍历的时候被访问到，只有一次

如果统计一个点的贡献的复杂度为O(1)的话，该算法的复杂度为O(nlogn)。