反演变换的性质

反演本质上是一种几何变换，常见的几何变换还有平移、旋转、反射……

反演变换适用于题目中存在多个圆/直线之间的相切关系的情况。利用反演变换的性质，在反演空间求解问题，可以大幅简化计算。这篇文章主要介绍反演的定义和一些常用性质

一、定义

设O是平面π上的一个定点，k是一个非零常数，如果平面π的一个变换，使得对于平面π上任意异于点O的点A与其像点A'，恒有

（1）A'，O，A共线

（2）

则这个变换称为平面的一个反演变换，记作I(O,k)，其中定点O称为反演中心，常数 k 称为反演幂，点A'称为A的反点；

反演中心本身不参与反演变换，反演后，反演中心O仍记为O；

当反演幂k>0时，反演变换I(O,k)称为双曲型反演变换；当k<0时，反演变换I(O,k)称为椭圆型反演变换；

对于反演变换I(O,k)，令，则以反演中心O为圆心，r为半径的圆称为反演变换I(O,k)的反演圆或基圆，r称为反演半径。

就像下面这样

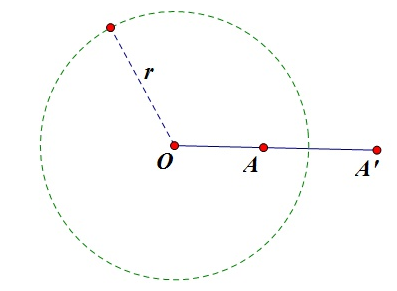
（这是反演幂k大于0的情况，k小于0的情况类似）

二、性质

性质1：反演变换可逆

由反演的定义可知，当A'是A的反点时，点A也是A'的反点，所以点A与点A'互为反点

性质2：

（1）位于反演圆上的点，保持在原处；

（2）位于反演圆内的点，变换为反演圆外的点；

（3）位于反演圆外的点，变换为反演圆内的点；

以上是每个点经过反演后的性质，接下来我们讨论直线和圆经过反演后的图形

性质3：

（1）过反演中心的直线反演后为自身（不包含反演中心）

（2）不过反演重心的直线，反演后为过反演中心的圆

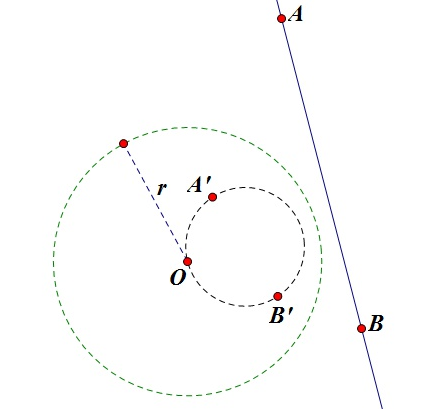
性质4：不过反演中心的圆，反演后仍为一个圆，且与原来的圆关于反演中心位似

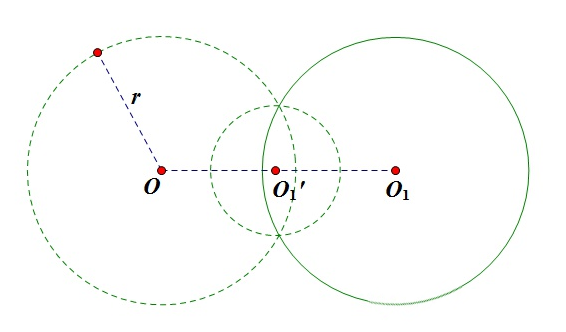
（注意，这里的的反演点并不是，这里加虚线的意思仅表示两圆关于点O位似）

性质5：过反演中心的圆，反演后为不过反演中心的一条直线，且该直线平行于原来的圆在反演中心处的切线

然后反演还有一个非常重要的性质

性质6：两条直线或曲线的夹角大小在反演变换下是不变的

当然，如果叙述完整，引入有向角的概念，那么反演后的夹角大小相等，方向相反

这一性质通常也被称为反演的反向保角性。

大家掌握这些基本知识，就可以用反演变换解决平面几何的相关问题了。