当你从一个顶点开始,沿着某条路往下走,一直走到底,如果走完后发现不能达到目标解,就回溯,返回到上一个节点,换条路,然后继续走到底,如此往复,直至所有可能的结果都被搜索完。通俗理解就是不撞南墙不回头这种感觉,这个就是我们这篇要讲解的内容,下面带领大家结合实例系统的学习一下。
一、什么是DFS?
DFS简单讲叫深度优先搜索,就是指:优先考虑深度,换句话说就是一条路走到黑,直到无路可走的情况下,才会选择回头,然后重新选择一条路。
二、DFS的实现
原理:DFS是由栈的形式实现的,通过栈进行路径储存。
DFS的实现步骤:
(1)从顶点出发。
(2)访问顶点,也就是根节点。
(3)依次从顶点的未被访问的邻接点出发,进行深度优先遍历;直至和顶点有路径相通的顶点都被访问。
(4)若此时尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优遍历,直到所有顶点均被访问过为止。
三、DFS的注意事项
(1)剪枝 剪枝是为了减少时间成本
(2)回溯 回溯回到原来路径
(3)还原 回到原来路径时,要还原现场
四、基础案例
题目描述:马在中国象棋以日字形规则移动。
请编写一段程序,给定 n∗m 大小的棋盘,以及马的初始位置 (x,y),要求不能重复经过棋盘上的同一个点,计算马可以有多少途径遍历棋盘上的所有点。
输入格式:第一行为整数 T,表示测试数据组数。
每一组测试数据包含一行,为四个整数,分别为棋盘的大小以及初始位置坐标 n,m,x,y。
输出格式:每组测试数据包含一行,为一个整数,表示马能遍历棋盘的途径总数,若无法遍历棋盘上的所有点则输出 0。
数据范围:
1≤T≤9,
1≤m,n≤9,
0≤x≤n−1,
0≤y≤m−1
输入样例:
1
5 4 0 0
输出样例:
32
题解(DFS)分析:马只能走“日”字形,那么移动一次只能有八种情况出现,如图所示。
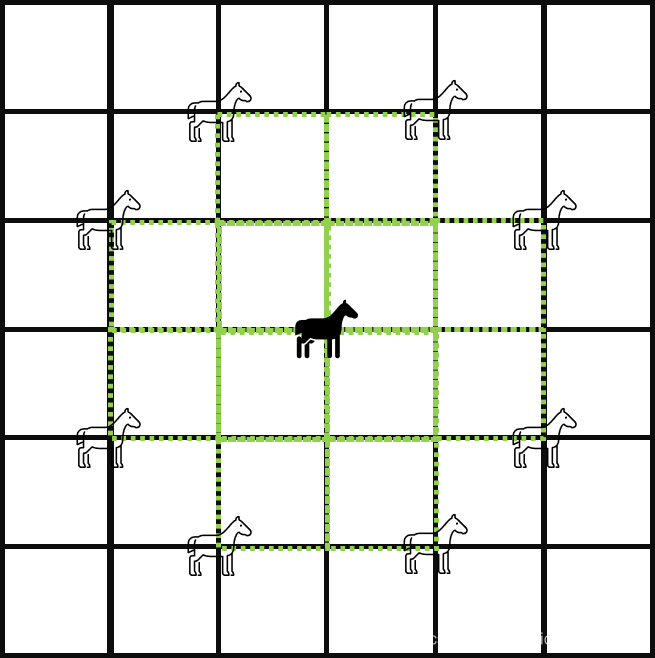
很显然,是DFS模型的变形,把可以到达的邻接点距离写成数组,再分析题目,由于要寻找多条道路,故每次寻路完毕需要进行回溯。贴上代码。
#include <iostream>
#define xa x + a[i]
#define yb y + b[i]
using namespace std;
int m, n, x, y, cnt = 0;
const int a[]={1,2,2,1,-1,-2,-2,-1};
const int b[]={2,1,-1,-2,-2,-1,1,2};
bool g[10][10];
void dfs(int x, int y, int dc){
if(dc == 0){
cnt ++;
return;
}
g[x][y] = true;
for(int i = 0; i < 8; i++){
if(xa >= 0 && xa < m && yb >= 0 && yb < n && !g[xa][yb])
dfs(xa, yb, dc - 1);
}
g[x][y] = false;
}
int main(){
int t = 0;
cin >> t;
while(t--){
cin >> m >> n >> x >> y;
dfs(x, y, n * m - 1);
cout << cnt << endl;
cnt = 0;
}
return 0;
}
| 1702 | 数据结构-图的遍历-DFS深度优先搜索(深搜) |
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程