(1)堆的概念
所谓堆,它是一个数组,也能够被看成一个近似的全然二叉树。树上每一个结点相应数组的一个元素。二叉堆分为二种:最大堆和最小堆。本文主要介绍最大堆,最小堆类似。最大堆的特点:对于随意某个结点,该结点的值大于左孩子、右孩子的值,可是左右孩子的值没有要求。
(2)堆排序算法
堆排序算法调用函数Build_max_heap将输入数组array[1..n]建立成堆。当中n表示数组长度。由于建立堆后,数组的最大元素被存放在根节点A[1],通过将A[1]与数组最后一个元素进行交换。将最大元素后移,实现排序。
可是,交换后新的根节点可能不满足堆的特点,所以须要调用子函数Max_heapify对剩余的数组元素进行最大堆性质的维护。堆排序算法。通过不断反复这个过程(n-1)次,实现数组的从小到大排序(由于採用最大堆)。
对于上面提及的两个子函数进行简要介绍。
函数Build_max_heap的作用:建堆。
由于子数组A(n/2+1..n)是树的叶子节点,不须要进行堆的维护。
所以。仅仅须要对A[1..n/2]数组元素进行维护。就可构建堆。
函数Max_heapify的作用:维护堆。过程:如果A[i]表示树的某个结点,则A[2*i]是其左孩子,A[2*i+1]是其右孩子。接下来,比較三者大小挑选出最大元素的下标,存放于largest。然后。推断(largest==i)吗。若不满足则进行元素交换。将大的元素上移。
此时,以A[largest]为根节点的子树可能不满足堆的性质,所以须要递归调用自身。
(3)动图演示:
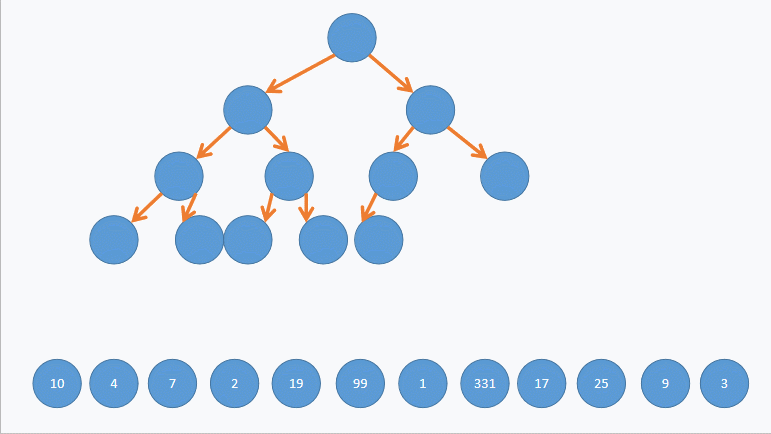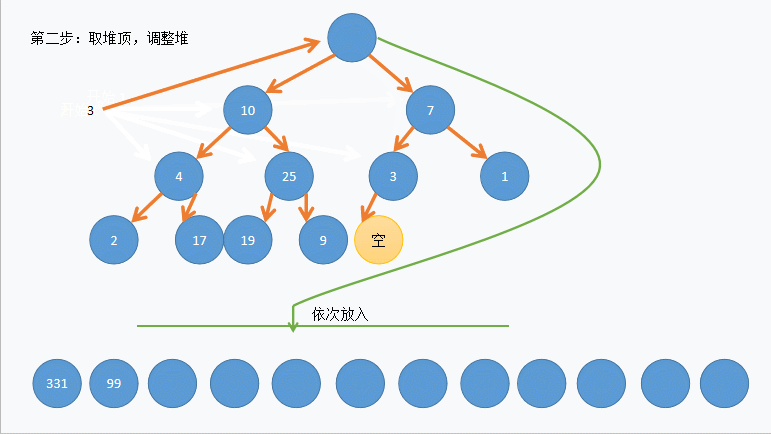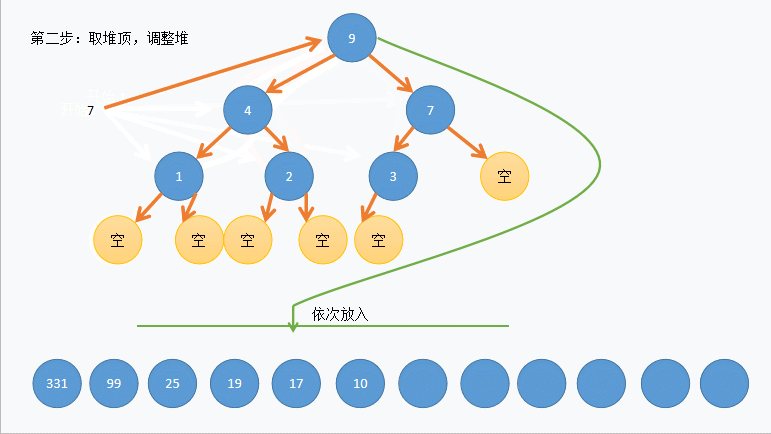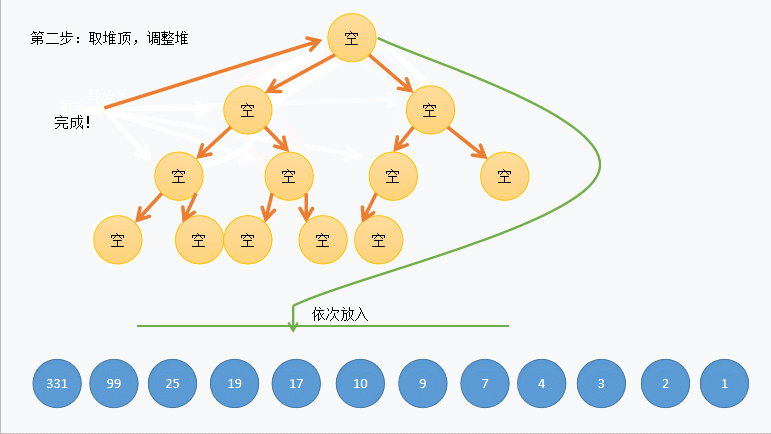
(4)C语言代码实现如下:
#include <stdio.h>#include <stdlib.h>void swap(int *arr,int i, int k) {
int temp = arr[i];
arr[i] = arr[k];
arr[k] = temp;}void max_heapify(int *arr, int start, int end) {
//建立父节点下标和子节点下标
int dad = start;
int son = dad * 2 + 1;
while (son <= end)
{ //若子节点下标在范围内才做比较
if (son + 1 <= end && arr[son] < arr[son + 1]) //先比较两个子节点大小,选择最大的
{
son++;
}
if (arr[dad] > arr[son]) //如果父节点大于子节点代表调整完毕,直接跳出
{
return;
}
else
{ //否则交换父子节点的值再继续左右子节点值得比较
swap(arr,dad, son);
printf("dad=%d--son=%d\n",dad,son);
dad = son;
son = dad * 2 + 1;
}
}}void heap_sort(int *arr, int len) {
int i;
//初始化,i从最后一个父节点开始调整
for (i = len / 2 - 1; i >= 0; i--)
{
max_heapify(arr, i, len - 1);
}
for (i = len - 1; i > 0; i--)
{
swap(arr,0, i);
max_heapify(arr, 0, i - 1);
}}int main(int argc, char const *argv[]){
int arr[] = {5,3,8,1,6};
int len = sizeof(arr) / sizeof(int);
heap_sort(arr, len);
for (int i = 0; i < len; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
return 0;}如果我们编译并运行上述程序,那么它应该产生以下结果:
dad=1--son=4 dad=0--son=2 dad=0--son=1 dad=0--son=2 dad=0--son=1 1 3 5 6 8
| 1718 | 数据结构-堆排序 |
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程