本篇主要是围绕着递归算法的概念、实质、思想以及设计要素四个方向叙述,同时通过实例讲解,促进大家对递归算法的理解。
一、算法概念
递归算法是一种直接或者间接调用自身函数或者方法的算法。说简单了就是程序自身的调用。
二、算法实质
递归算法就是将原问题不断分解为规模缩小的子问题,然后递归调用方法来表示
问题的解。(用同一个方法去解决规模不同的问题)
三、算法思想
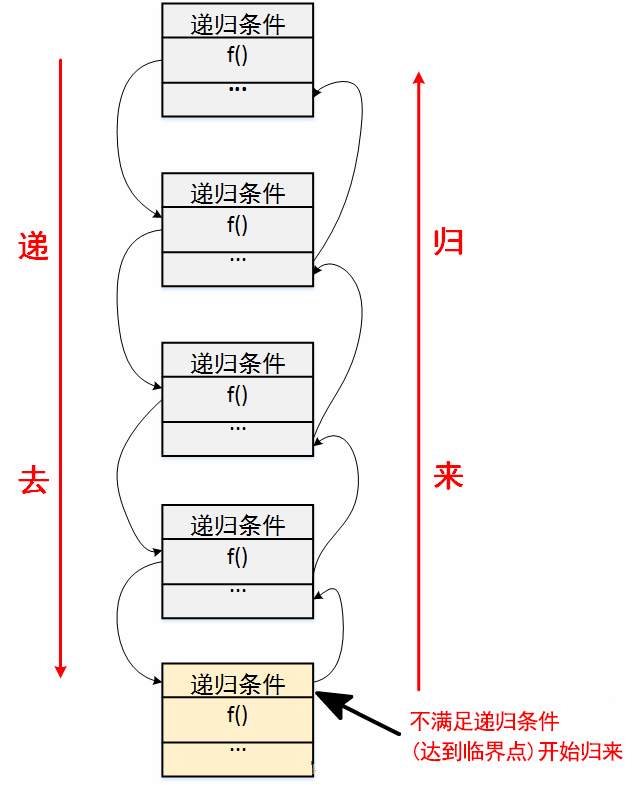
递归算法,顾名思义就是有两个大的阶段:递和归,即就是有去(递去)有回(归来)。
递去:将递归问题分解为若干个规模较小,与原问题形式相同的子问题,这些子问题可以用相同的解题思路来解决
归来:当你将问题不断缩小规模递去的时候,必须有一个明确的结束递去的临界点(递归出口),一旦达到这个临界点即就从该点原路返回到原点,最终问题得到解决。
递归的图解分析
四、递归算法的设计要素
递归思维是一种从下向上的思维方式,使用递归算法往往可以简化我们的代码,而且还帮我们解决了很复杂的问题。递归算法的难点就在于它的逻辑性,一般设计递归算法需要考虑以下几点:
(1)明确递归的终止条件
(2)提取重复的逻辑,缩小问题的规模不断递去
(3)给出递归终止时的处理办法
五、递归算法的经典实例
(1)阶乘
n! = n * (n-1) * (n-2) * ...* 1(n>0)
//阶乘
int recursive(int i)
{
int sum = 0;
if (0 == i)
return (1);
else
sum = i * recursive(i-1);
return sum;
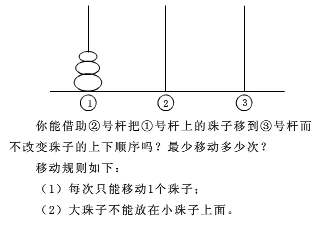
}(2)河内塔问题
(3)全排列
从n个不同元素中任取m(m≤n)个元素,按照一定的顺序排列起来,叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。
如1,2,3三个元素的全排列为:
1,2,3
1,3,2
2,1,3
2,3,1
3,1,2
3,2,1
//全排列
inline void Swap(int &a,int &b)
{
int temp=a;
a=b;
b=temp;
}
void Perm(int list[],int k,int m)
{
if (k == m-1)
{
for(int i=0;i<m;i++)
{
printf("%d",list[i]);
}
printf("n");
}
else
{
for(int i=k;i<m;i++)
{
Swap(list[k],list[i]);
Perm(list,k+1,m);
Swap(list[k],list[i]);
}
}
}(4)斐波那契数列
斐波纳契数列,又称黄金分割数列,指的是这样一个数列:1、1、2、3、5、8、13、21、……
这个数列从第三项开始,每一项都等于前两项之和。
有趣的兔子问题:
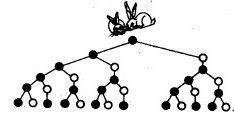
一般而言,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有兔子都不死,那么一年以后可以繁殖多少对兔子?
分析如下:
第一个月小兔子没有繁殖能力,所以还是一对;
两个月后,生下一对小兔子,总数共有两对;
三个月以后,老兔子又生下一对,因为小兔子还没有繁殖能力,总数共是三对;
……
依次类推可以列出下表:
| 经过月数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 幼崽对数 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 |
| 成兔对数 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 |
| 总体对数 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 |
//斐波那契
long Fib(int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
if (n > 1)
return Fib(n-1) + Fib(n-2);
}| 1004 | [递归]母牛的故事 |
| 1575 | 蓝桥杯算法提高VIP-递归倒置字符数组 |
| 2217 | 蓝桥杯算法训练-递归求二项式系数值 |
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程