图论 (Graph theory) 是数学的一个分支,图是图论的主要研究对象。图 (Graph) 是由若干给定的顶点及连接两顶点的边所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系。顶点用于代表事物,连接两顶点的边则用于表示两个事物间具有这种关系。
图(graph)是数据结构和算法学中最强大的框架之一。图几乎可以用来表现所有类型的结构或系统,从交通网络到通信网络,从下棋游戏到最优流程,从任务分配到人际交互网络,图都有广阔的用武之地。而要进入图论的世界,清晰、准确的基本概念是必须的前提和基础。
下面对其最核心和最重要的概念作出说明。关于图论的概念异乎寻常的多,先掌握下面最核心最重要的,足够开展一些工作了,其它的再到实践中不断去理解和熟悉吧。
图(graph)并不是指图形图像(image)或地图(map)。通常来说,我们会把图视为一种由“顶点”组成的抽象网络,网络中的各顶点可以通过“边”实现彼此的连接,表示两顶点有关联。注意上面图定义中的两个关键字,由此得到我们最基础最基本的2个概念,顶点(vertex)和边(edge),如图所示。
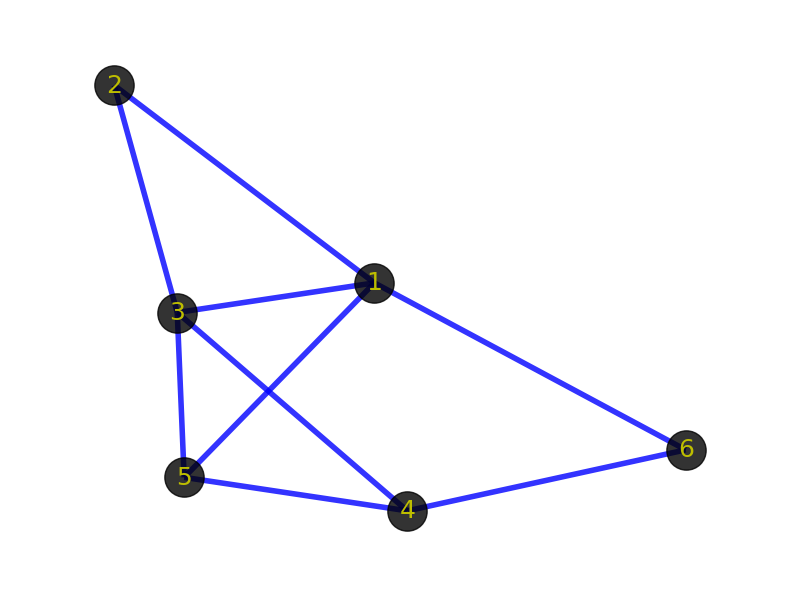
一、顶点(vertex)
上图中黑色的带数字的点就是顶点,表示某个事物或对象。由于图的术语没有标准化,因此,称顶点为点、节点、结点、端点等都是可以的。叫什么无所谓,理解是什么才是关键。
二、边(edge)
上图中顶点之间蓝色的线条就是边,表示事物与事物之间的关系。需要注意的是边表示的是顶点之间的逻辑关系,粗细长短都无所谓的。包括上面的顶点也一样,表示逻辑事物或对象,画的时候大小形状都无所谓。
三、同构(Isomorphism )
先看看下面2张图:
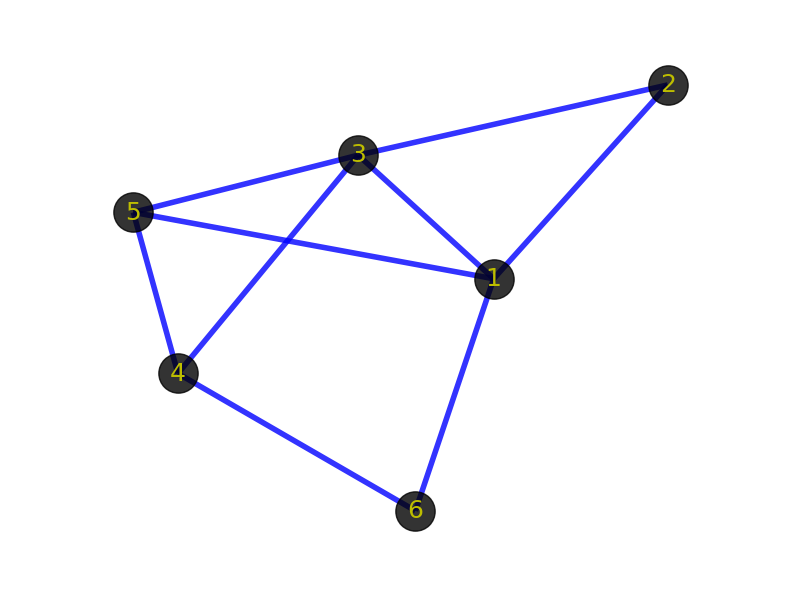
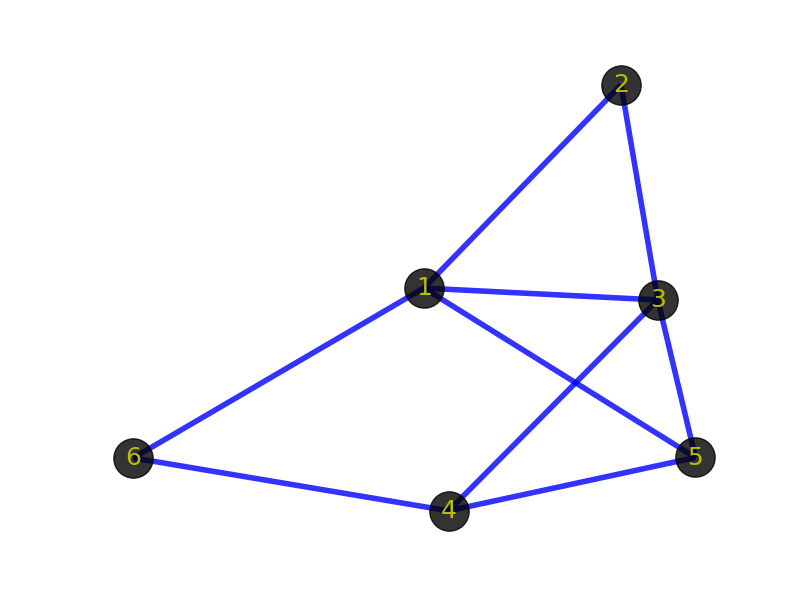
首先你的感觉是这2个图肯定不一样。但从图(graph)的角度出发,这2个图是一样的,即它们是同构的。前面提到顶点和边指的是事物和事物的逻辑关系,不管顶点的位置在哪,边的粗细长短如何,只要不改变顶点代表的事物本身,不改变顶点之间的逻辑关系,那么就代表这些图拥有相同的信息,是同一个图。同构的图区别仅在于画法不同。
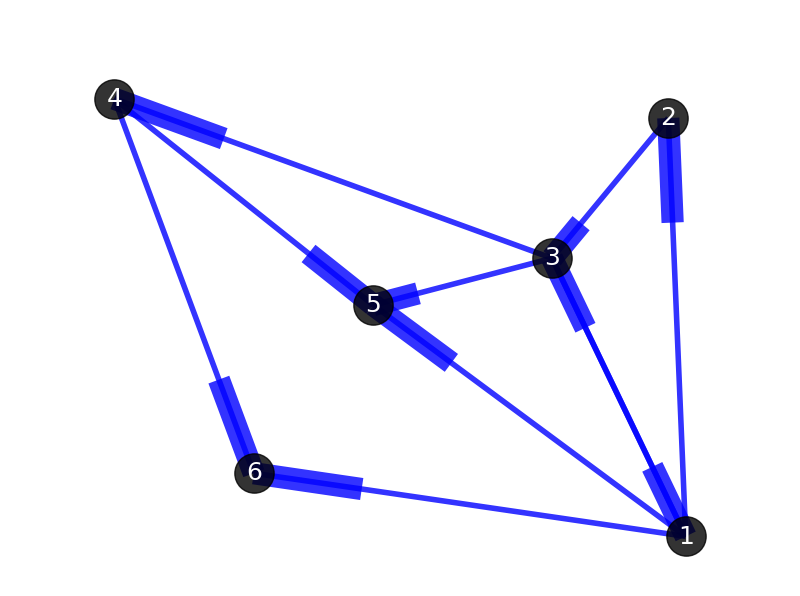
四、有向/无向图(Directed Graph/ Undirected Graph)
最基本的图通常被定义为“无向图”,与之对应的则被称为“有向图”。两者唯一的区别在于,有向图中的边是有方向性的。下图即是一个有向图,边的方向分别是:(1->2), (1-> 3), (3-> 1), (1->5), (2->3), (3->4), (3->5), (4->5), (1->6), (4->6)。要注意,图中的边(1->3)和(3->1)是不同的。有向图和无向图的许多原理和算法是相通的。
五、权重(weight)
边的权重(或者称为权值、开销、长度等),也是一个非常核心的概念,即每条边都有与之对应的值。例如当顶点代表某些物理地点时,两个顶点间边的权重可以设置为路网中的开车距离。下图中顶点为4个城市:Beijing, Shanghai, Wuhan, Guangzhou,边的权重设置为2城市之间的开车距离。有时候为了应对特殊情况,边的权重可以是零或者负数,也别忘了“图”是用来记录关联的东西,并不是真正的地图。
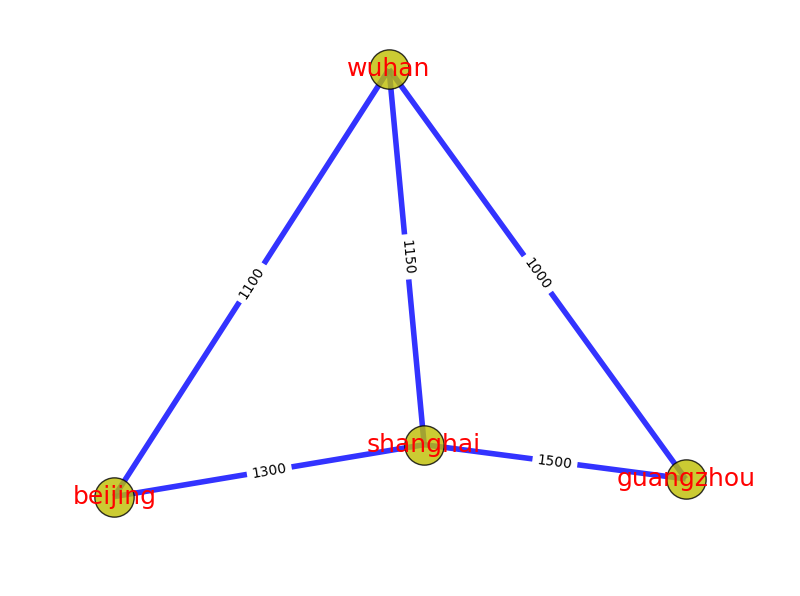
六、路径/最短路径(path/shortest path)
在图上任取两顶点,分别作为起点(start vertex)和终点(end vertex),我们可以规划许多条由起点到终点的路线。不会来来回回绕圈子、不会重复经过同一个点和同一条边的路线,就是一条“路径”。两点之间存在路径,则称这2个顶点是连通的(connected)。
还是上图的例子,北京->上海->广州,是一条路径,北京->武汉->广州,是另一条路径,北京—>武汉->上海->广州,也是一条路径。而北京->武汉->广州这条路径最短,称为最短路径。
路径也有权重。路径经过的每一条边,沿路加权重,权重总和就是路径的权重(通常只加边的权重,而不考虑顶点的权重)。在路网中,路径的权重,可以想象成路径的总长度。在有向图中,路径还必须跟随边的方向。
值得注意的是,一条路径包含了顶点和边,因此路径本身也构成了图结构,只不过是一种特殊的图结构。
七、环(loop)
环,也成为环路,是一个与路径相似的概念。在路径的终点添加一条指向起点的边,就构成一条环路。通俗点说就是绕圈。
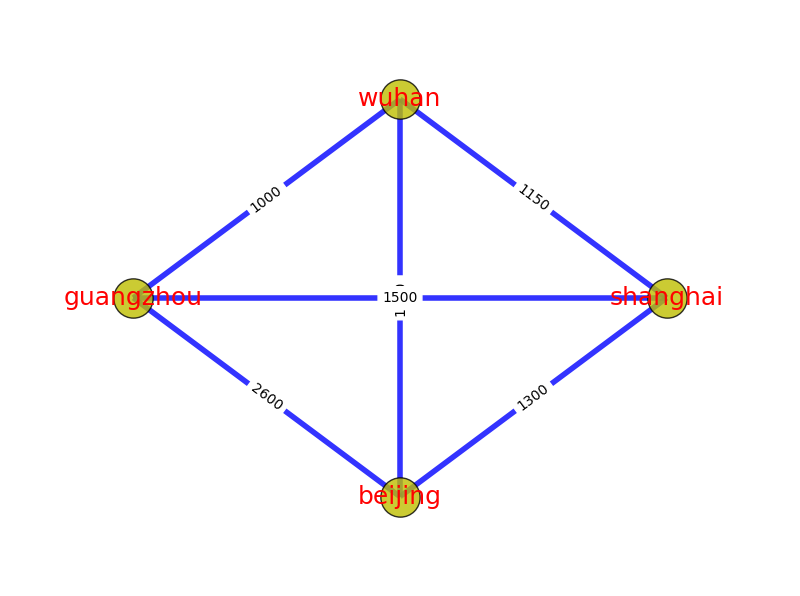
上图中,北京->上海->武汉->广州->北京,就是一个环路。北京->武汉->上海->北京,也是一个环路。与路径一样,有向图中的环路也必须跟随边的方向。环本身也是一种特殊的图结构。
八、连通图/连通分量(connected graph/connected component)
如果在图G中,任意2个顶点之间都存在路径,那么称G为连通图(注意是任意2顶点)。上面那张城市之间的图,每个城市之间都有路径,因此是连通图。而下面这张图中,顶点8和顶点2之间就不存在路径,因此下图不是一个连通图,当然该图中还有很多顶点之间不存在路径。
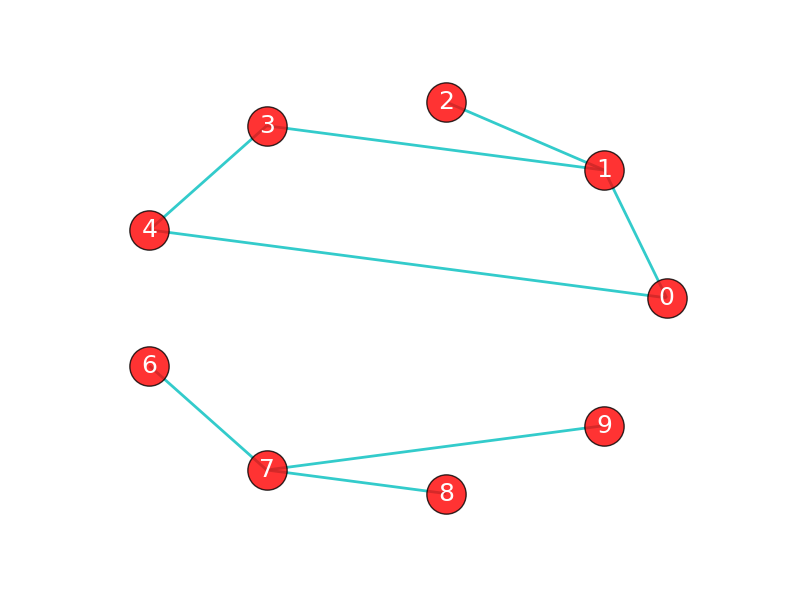
上图虽然不是一个连通图,但它有多个连通子图:0,1,2顶点构成一个连通子图,0,1,2,3,4顶点构成的子图是连通图,6,7,8,9顶点构成的子图也是连通图,当然还有很多子图。我们把一个图的最大连通子图称为它的连通分量。0,1,2,3,4顶点构成的子图就是该图的最大连通子图,也就是连通分量。连通分量有如下特点:
(1)是子图;
(2)子图是连通的;
(3)子图含有最大顶点数。
注意:“最大连通子图”指的是无法再扩展了,不能包含更多顶点和边的子图。0,1,2,3,4顶点构成的子图已经无法再扩展了。
显然,对于连通图来说,它的最大连通子图就是其本身,连通分量也是其本身。
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程